I Leistung im Wechselstromkreis mit Ohm'schem Widerstand
Bei Wechselstrom kommt es in der Regel je nach den vorhandenen Bauteilen
im Wechselstromkreis zu Phasenverschiebungen zwischen Stromstärke und
Spannung. Wenn jedoch nur ein Ohm'scher Widerstand im Stromkreis
ist, sind U(t) und I(t) gleichphasig (z.B. I(t) = I0·sin(ω·t)
und U(t) = U0·sin(ω·t)), und wir brauchen gegenüber dem
Gleichstromfall nur wenig hinzulernen. Es gilt nämlich für die von der
Energiequelle gelieferte oder vom Widerstand aufgenommene Leistung
P(t) = U(t)·I(t) = U0·I0·sin2(ω·t)
Die Leistung P ist zeitabhängig. Sie pulsiert im Rhythmus von 100 Hz
(Abb. 1), ist aber nie negativ, d.h. die Energiequelle führt dem
Widerstand abgesehen von einigen regelmäßigen Zeitpunkten immer (positive)
Energie zu. Es könnte sinnvoll sein, den zeitlichen Mittelwert über eine
Periode zu betrachten. Weil der Mittelwert <sin2(ω·t)> =
1/2 ist, gilt also <P(t)> = 1/2·U0·I0. Bis auf
den Faktor 1/2 ist das wie im Gleichstromfall. Das motivierte für die
Definition der Effektivwerte:
<P(t)> = Ueff · Ieff,
wobei Ueff = U0/√2
und Ieff = I0/√2.
|
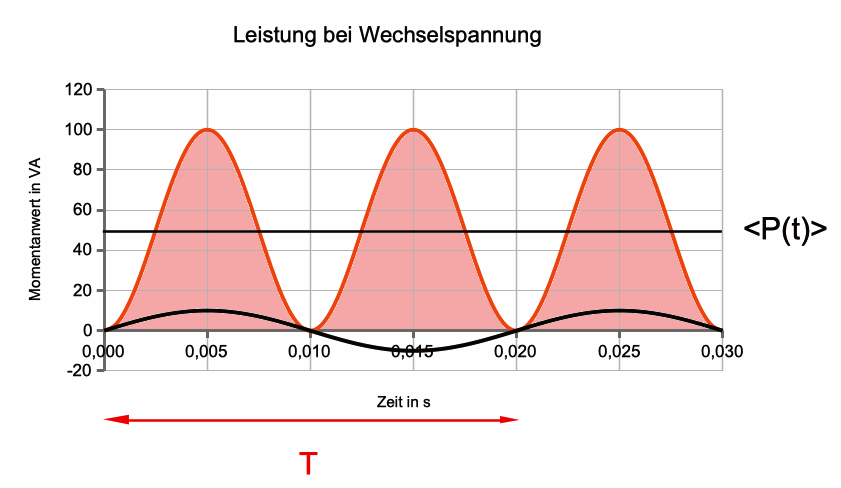
Abb. 1: Leistung P(t) bei rein Ohm'schem Widerstand
(rot). Die zeitlich gemittelte Leistung <P(t)> ist als
horizontale Strecke eingezeichnet, zusätzlich noch der Zeitverlauf
von Spannung oder Stromstärke (schwarz). Die Periode der Spannung
(hier 0,02s, entsprechend der Frequenz 50 Hz) ist doppelt so groß
wie die Periode von 0,01 s der Leistung P(t).
Das Vorzeichen der Leistung ist durch die Einfärbung erkennbar. Bei
einem rein Ohm'schen Widerstand fließt zu fast allen Zeit Energie
(erkennbar an der nie negativen Leistung P(t)) von der Energiequelle
zum Widerstand (rötlich eingefärbt). Niemals fließt Energie vom
Verbraucher zur Energiequelle zurück.
|
II Wirkleistung, Scheinleistung und Blindleistung in
allgemeinen Fällen
( zurück
)
|
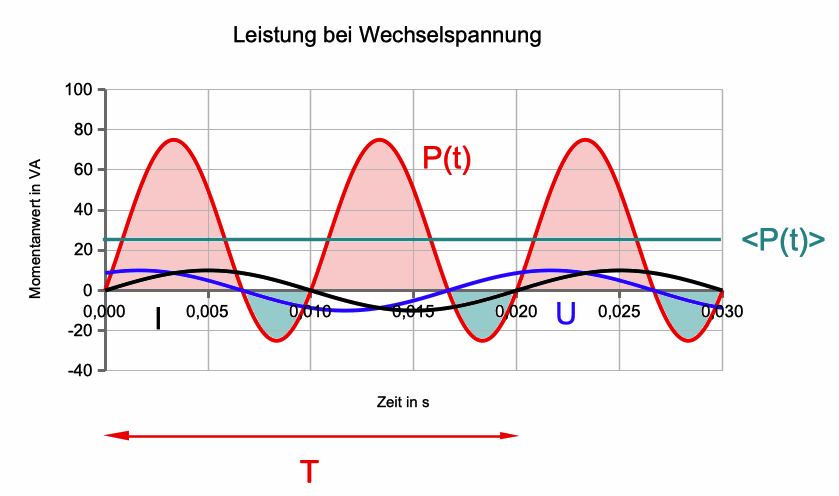
Abb. 2: Der Verbraucher enthält Widerstände und
Spulen oder Kondensatoren: momentane Leistung P(t) (rot). Es gibt
eine Phasenverschiebung zwischen Stromstärke und Spannung (z.B. I(t)
= I0·sin(ω·t) und U(t) = U0·sin(ω·t + φ)). In
der Zeichnung ist φ = 600.
Die zeitlich gemittelte Leistung <P(t)>, sie wird Wirkleistung
genannt (türkis), ist als horizontale Strecke eingezeichnet.
Sie ist deutlich geringer als die Wirkleistung bei rein Ohm'schem
Verbraucher (Abb.1). Der Zeitverlauf von Spannung und Stromstärke
(blau und schwarz) ist ebenfalls eingezeichnet. Die Periode T der
Spannung bzw. Stromstärke (hier 0,02s, entsprechend der Frequenz 50
Hz) ist doppelt so groß wie die Periode von 0,01 s der Leistung
P(t).
An der Einfärbung erkennst du, in welchen Zeitintervallen Energie
von der Energiequelle zum Verbraucher fließt (P(t) > 0; rötlich)
und in welchen Zeitintervallen Energie vom Verbraucher zur
Energiequelle zurück fließt (P(t) < 0; bläulich).
|
Die Energiequelle muss mehr elektrische Energie liefern, als der
Verbraucher dauerhaft aufnimmt, als genutzt werden kann. In der Praxis
bedeutet das, dass größere Generatoren, Transformatoren und für stärkeren
Strom ausgelegte Leitungen benötigt werden. Das spielt auch eine wichtige
Rolle bei der Einspeisung aus alternativen Energiequellen.
Es müssen komplizierte Maßnahmen getroffen werden, um die
Phasenverschiebung möglichst gering zu halten.
Wenn zwischen Spannung und Stromstärke eine Phasenverschiebung (φ
≠ 0) existiert, wie z.B., wenn Kondensatoren oder Spulen, also auch
Elektromotoren, im Stromkreis sind, muss der zeitliche
Mittelwert der Leistung durch Integration ermittelt werden.
Du erhältst damit die für die Energieversorgung wichtige Gesetzmäßigkeit
für die Wirkleistung
| P = <P(t)> =U0·I0 ·1/2 · cos(φ)
= Ueff · Ieff · cos(φ) |
mit dem berühmt/berüchtigten Phasenfaktor
oder Leistungsfaktor cos(φ).
Als Scheinleistung wird definiert S = Ueff · Ieff,
und als Blindleistung Q = √[S2 - P2] = Ueff
· Ieff ·√[1 - cos2(φ)] = Ueff ·
Ieff ·sin(φ).
Im Allgemeinen ist die (nutzbare) Wirkleistung geringer als die
Scheinleistung. Elektrizitätswerke und die Netze müssen aber so ausgelegt
sein, dass sie die Scheinleistung liefern können, also mehr als die
Wirkleistung, obwohl sie den Überschuss, abgesehen von Verlusten, wieder
zurückbekommen. Blindleistung und Scheinleistung belasten die Netze und
sorgen für größere Verluste. Der Leistungsfaktor ist ein Maß dafür, wie
sich Wirkleistung und Scheinleistung unterscheiden. Ziel ist ein
Leistungsfaktor cos(φ) nahe 1.
|
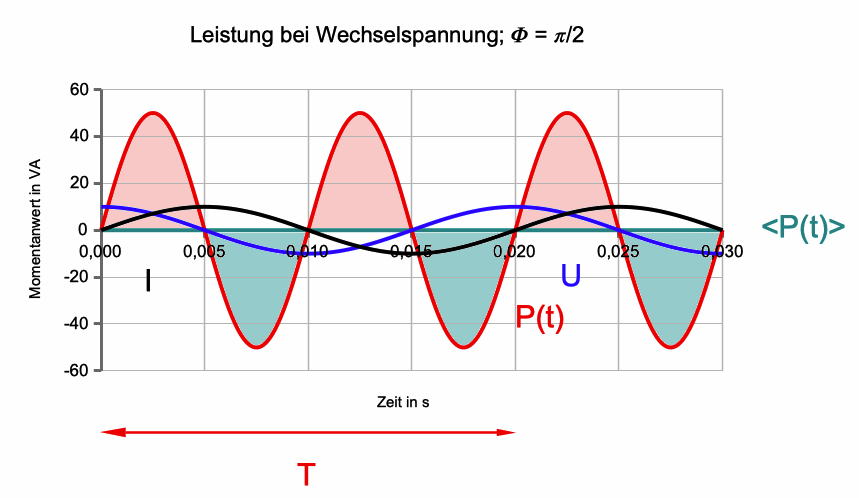
Abb. 3: Leistung bei rein induktiver Last (φ = π/2)
Bei einem rein induktiven Verbraucher (ideale Spule, z.B.
eines idealen Transformators) ist cos(φ) = 0. Die Spule nimmt dann -
trotz beträchtlichen Scheitelwerts der Stromstärke - keine Energie
dauerhaft auf (Wirkleistung P = <P(t)> = 0), aber die
Energiequelle muss evtl. große Leistung zur Verfügung stellen, die
sie ganz wieder zurück nimmt. |
Bei der Beurteilung des Energiebedarfs geht es also nicht nur um die
Betrachtung des "Verbrauchs" (Privathaushalte zahlen nur für die mit
der Wirkleistung verbundene Energie), sondern auch um die mit
teils hohen Kosten verbundenen zusätzlichen Leistungen (Blindleistung und
auch Regelleistung zur Stabilhaltung der Netzfrequenz in engen Toleranzen
um 50 Hz). Hier sind Maßnahmen gefordert, die schnell zu- und abgeschaltet
werden können.
Es gilt also
<P(t)> =U0·I0/T ∫ sin(ω·t +
φ)·sin(ω·t)·dt , integriert über eine volle Periode der Länge T. Den
Additionstheoremen der Trigonometrie entnimmst du sin(x)·sin(y) = 1/2 ·
[cos(x-y)- cos(x+y)]. Dann wird der Integrand sin(ω·t + φ)·sin(ω·t)
= 1/2 · [cos(x-y) - cos(x+y)] = 1/2 · [cos(φ) - cos(2ω·t + φ)].
Der erste Anteil zum Integral liefert 1/2 · cos(φ) ·T, der zweite Anteil
verschwindet. Es ergibt sich <P(t)> =U0·I0
·1/2 · cos(φ) = Ueff · Ieff · cos(φ).
( Februar 2021 )


