|
SG001 Ort x im
Unterschied zu Weg s |
Impres-sum |
Bis ins Mittelalter hinein konnte man Bewegungen nur durch die Angaben "schneller" oder "langsamer" beschreiben. Mit solchen vagen Aussagen konnte man Bewegung nicht vernünftig verstehen. Erst nachdem ein Bischof, Nikolaus von Oresme, im 14. Jahrhundert vorgeschlagen hatte, Bewegungen durch die Veränderung von Koordinaten zu beschreiben, war ein Fortschritt möglich. 300 Jahre später war Newton damit in der Lage, erstmals in der Geschichte der Menschheit, zu einem exakten und vollständigen Verständnis eines Teilgebiets der Physik zu kommen, der Mechanik.
Früher stellte man - nach den Vorschlägen von Nikolaus von Oresme und Descartes - mathematisch und mit Hilfe von Graphen Geschwindigkeiten v und zurückgelegte Wege s in Abhängigkeit von der Zeit dar. Man stellte sich vor, dass die Bewegung zu irgendeinem Zeitpunkt beginnt, heute würden wir das die Zeit 0 nennen, und dass man untersucht, welche Strecke oder welchen Weg s von da aus der bewegte Körper bis zu einem anderen Zeitpunkt, t, zurückgelegt hat.
Wenn du dich mit einer Freundin oder einem Freund treffen möchtest und sagst nur, wir wollen uns nach einem Weg s = 2 km um 3 Uhr treffen, verfehlt ihr euch höchstwahrscheinlich. Denn niemand kann sich allein auf diese Aussage hin vorstellen, in welcher Richtung sich der Treffpunkt befindet. Das gilt sogar bei einer eindimensionalen (linearen) Bewegung: Auf welcher Seite des Startpunkts soll denn der Treffpunkt liegen?
Wenn du 5 km in eine bestimmte Richtung läufst und weiter
5 km zurück, befindest du dich wieder am Ausgangspunkt, am Ort x = 0,
wenn dort der Koordinatenursprung war. Aber du hast einen Weg s von 10
km zurück gelegt.
Die Angabe eines "zurückgelegten Weges s" hilft deshalb nur in Ausnahmefällen weiter.
. Heutzutage beschreibt man Bewegungen lieber mit dem Ort
x, der zur Zeit t erreicht ist. Und weil sich der Körper
i.A. in verschiedene Richtungen des Raums bewegen kann, wird der "erreichte
Ort" durch die drei Koordinaten x, y, z im Raum beschrieben.
Mathematisch fasst man die drei Koordinaten zu einem Vektor
x, dem Ortsvektor, zusammen. Die Vektoreigenschaft wird
durch Fettdruck ausgedrückt, oder, besonders in handschriftlichen
Texten, man zeichnet über
das Symbol x einen kleinen Pfeil, etwa so: ![]()
Wenn man dann eine Bewegung durch den Ort in Abhängigkeit
von der Zeit beschreiben möchte, schreibt man x(t) (x in
Fettdruck).
Bei einer Autofahrt kann der Ort mit Hilfe eines
GPS-Geräts, wie im Navi, gemessen werden, der zurückgelegte Weg mit dem
Kilometerzähler. In der englischen Sprache heißt Ort "position", und Weg
in vielen Fällen "distance". Ortsänderung Δx
heißt "displacement".
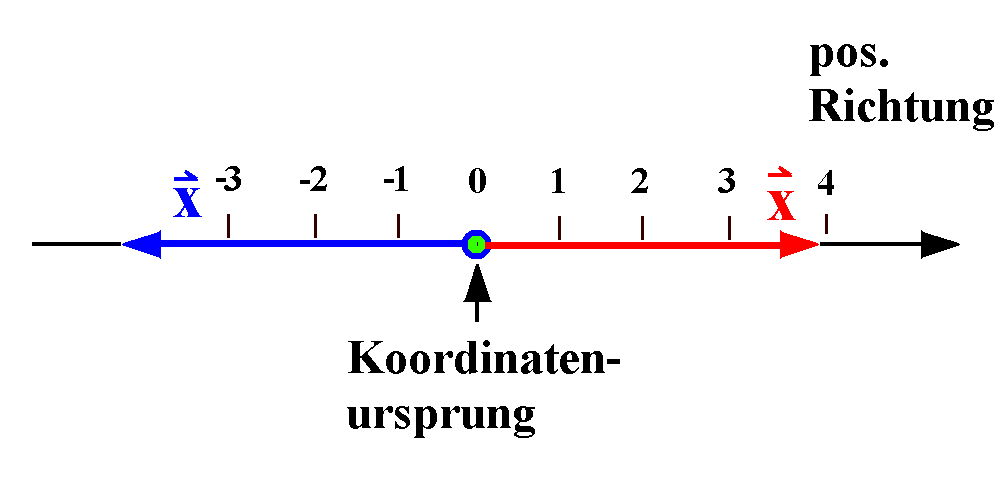 |
Bei einer eindimensionalen (linearen) Bewegung
gibt es nur zwei Möglichkeiten, in die der Ortsvektor x
(rot oder blau) zeigen kann.
Führt man ein Koordinatensystem mit Koordinatenursprung und positiver Koordinatenrichtung ein, kann man zwischen beiden Richtungen durch das Vorzeichen der Koordinate x unterscheiden.*) |
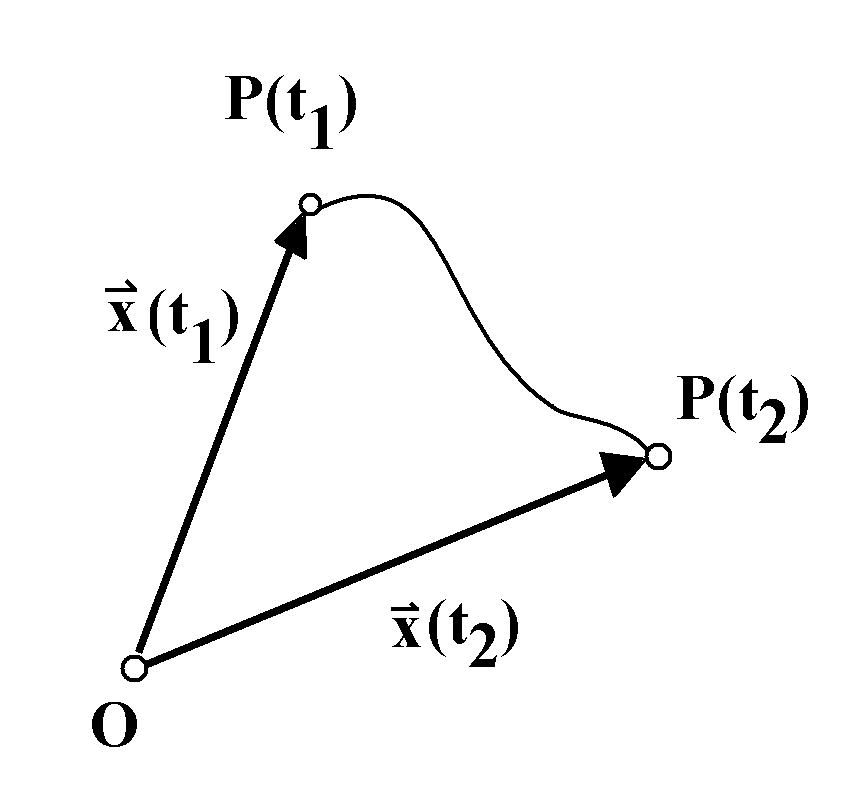 |
Zur Zeit t1 soll sich der Körper bei
P(t1) befinden, zur Zeit t2 bei P(t2).
Die Spitze des Ortsvektors x hat sich dabei von P(t1)
nach P(t2) fortbewegt. O ist der gemeinsame
Koordinatenursprung, an den alle Ortsvektoren "angeheftet" sind. Eine Bewegung beginnt in der Regel irgendwo, an einem so genannten Anfangsort x0. Das könnte der Ort zu einer Zeit t0 sein. Häufig wählt man t0 = 0. Dann wird zu diesem Zeitpunkt die Anzeige der Uhr auf 0 gestellt. |
Natürlich kann man auf eine der Koordinaten des Vektors x verzichten, wenn die Bewegung z.B. ausschließlich auf einer Tischplatte erfolgt (Bewegung in einer Ebene). Man kann auf 2 Koordinaten verzichten, wenn die Bewegung längs einer geraden Schiene oder einer Fahrbahn erfolgt (geradlinige Bewegung). Es verbleibt aber mindestens eine Koordinate, die sich im Lauf der Zeit t verändert. Sie wird in der Regel x(t) (ohne zusätzliches Vektorzeichen) genannt. x(t) kann positiv oder negativ oder auch 0 sein.
In vielen Schulbüchern ist auch heutzutage noch die Rede vom "zurückgelegten Weg s". Damit verwirren ihre Autoren manchmal ihre Leser, indem sie dann eigentlich die Ortskoordinate x oder den Ortsvektor x meinen. Wenn sie nach einem t-s-Graphen (bzw. s(t)-Graphen) fragen, erwarten sie einen t-x-Graphen. Die Entscheidung, was gemeint sein könnte, bleibt deinem Gespür überlassen.
Mit einer Aufgabe erklärst du dir den Unterschied
zwischen Ort x und Weg s. Eine beliebte Frage zu einem hüpfenden
Ball wird hier diskutiert.
Betrachte die Bewegung eines Massenpunktes auf einem Kreis
mit Radius r. Er startet zur Zeit 0 in einem bestimmten Punkt P. Wir
wählen P als Koordinatenursprung. Dann durchfährt der Massenpunkt
den Kreis und kommt zur Zeit t wieder
zum Punkt P zurück. Der zurückgelegte Weg entspricht dann dem
Kreisumfang, also gilt zur Zeit t: s(t) = 2·r·π.
Aber der Massenpunkt ist wieder im Koordinatenursprung, und für den Ort
zur Zeit t gilt x(t) = 0. Auch diese Überlegung macht dir den
Unterschied zwischen Ort und Weg klar.
|
Bewegungen werden durch die Angabe des Ortsvektors x
(bzw. der Ortskoordinate x) im Laufe der Zeit beschrieben. |
Diese 4 Größen solltest du sorgfältig auseinander halten:
|
Wesen |
Symbol |
Vorzeichen |
Information über |
|
| Ort (Ortsvektor) | Vektor | x(t) | (sinnlos) | Betrag und Richtung |
| vor allem bei
eindimensionalen Bewegungen: Ort(skoordinate) |
x-Koordinate des Ortsvektors x | x(t) | positiv, negativ und 0 | Betrag und Richtung des
Ortsvektors bei eindimensionalen Bewegungen. z.B. x(t) = - 4 m oder in einem anderen Fall: x(t) = 4 m ; Die Richtung wird durch das Vorzeichen ausgedrückt. |
| Betrag des Ortsvektors | Betrag des Ortsvektors x |
|x(t)| | nie negativ | z.B. |x(t)| = 4 m ; wohl nur als Abstand vom Koordinatenursprung brauchbar; keine Richtungsinformation |
| zurückgelegter Weg | Länge des zurückgelegten Wegs | s(t) | nie negativ | z.B. s(t) = 4 m (gemessen längs der Bahnkurve) |
Noch einmal: In der Physik werden zur Beschreibung von Bewegungen vor allem der Ort(svektor) x bzw. die Ortskoordinate x verwendet. Gelegentlich wird auch die Ortskoordinate y verwendet.
 |
Während "Wege" nur 0 oder positiv sein können und im
Laufe der Zeit niemals kleiner werden können, kann eine Ortskoordinate
auch negativ sein. Das setzt voraus, dass vor der Beschreibung oder
Untersuchung einer Bewegung ein Koordinatenursprung
vereinbart wurden, bei einer linearen Bewegung auch eine
positive Koordinatenrichtung. Das kann ganz
willkürlich geschehen, aber häufig vereinfacht eine bestimmte Wahl die
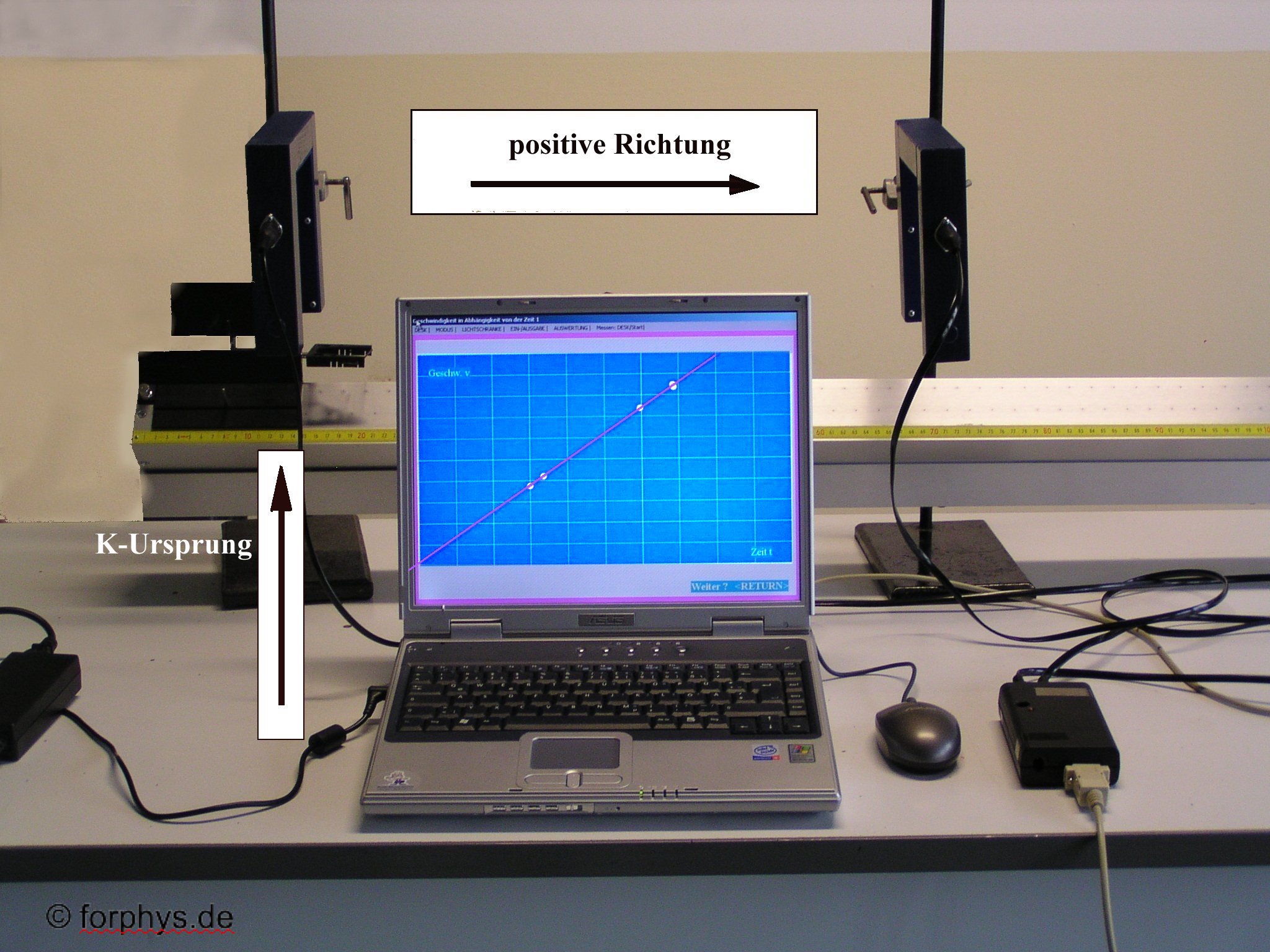
Überlegungen sehr stark. Ein Beispiel zeigt das Foto oben.
Im Foto wird mit zwei Lichtschranken die Laufzeit des
Gleiters von der ersten zur zweiten Lichtschranke gemessen und die
Geschwindigkeit beim Durchfahren der zweiten Lichtschranke. Mit dem
Interface rechts (schwarzes Kästchen) werden die Zeitmessungen
vorgenommen.
|
In der Regel muss vor der Untersuchung einer Bewegung ein Koordinatenursprung und eine positive Koordinatenrichtung vereinbart werden. |
Ist das geschehen, bedeutet eine positive Ortskoordinate, dass sich der Körper in positive Koordinatenrichtung vom Ursprung entfernt hat, eine negative Ortskoordinate, dass der Körper entgegengesetzt dazu vom Ursprung entfernt ist.
In vielen Fällen braucht man die 3 Koordinaten gar nicht zu kennen, sondern kann - viel einfacher - mit dem Ortsvektor x allein schon - "koordinatenfrei" - argumentieren. Dabei sind andere Vektoren wie der Geschwindigkeits- oder aber der Beschleunigungsvektor, v bzw. a, besonders nützlich.
*) Bei einer eindimensionalen Bewegung legt man einen Einheitsvektor ex fest, der den Betrag 1 hat und längs der positiven Koordinatenrichtung orientiert ist. Für den Ortsvektor x gilt dann: x = x · ex . x ist die Koordinate des Ortsvektors, die positiv und negativ sein kann. Ganz entsprechend: v = v · ex , a = a · ex .