|
SG038 Definition der Induktivität ©
H. Hübel Würzburg 2013
|
Es wird ein abschnittsweise linear wachsender und linear fallender Strom (ein Dreiecksstrom) durch eine Spule mit möglichst geringem Widerstand gepumpt. Die Spule reagiert darauf, indem sie eine Spannung induziert, eine Selbstinduktionsspannung, die unverfälscht gemessen wird.
Das wird ermöglicht mit einer so genannten Strompumpe, deren Details**) hier uninteressant sind. Im Allgemeinen ist es sehr schwer, einen Strom mit einem bestimmten Zeitverlauf durch eine Spule zu schicken.
 |
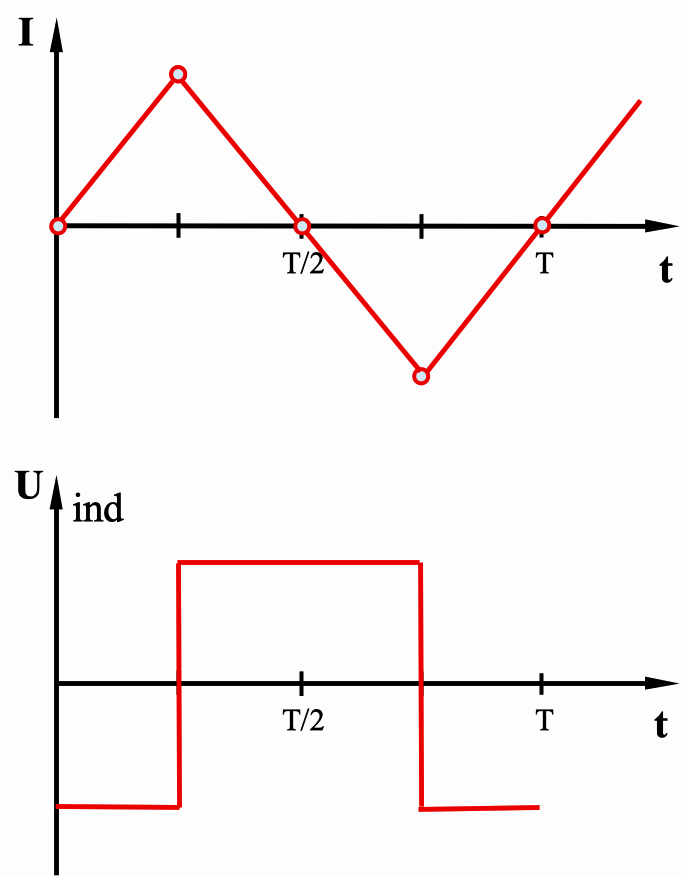Schickt man einen dreiecksförmigen Strom (links
oben) durch eine Spule, erzeugt diese eine abschnittsweise
konstante Selbstinduktionsspannung (links
unten).*) (Wenn die Spule weitgehend widerstandslos ist, wie die Schülerversuchsspule, stimmt die Selbstinduktionsspannung recht gut mit der Spannung an der Spule überein.) |
|
Uind prop ΔI/Δt
Die Proportionalitätskonstante wird definiert als Induktivität L:
| L = - Uind / ΔI/Δt |
L misst also die Selbstinduktionsspannung pro Änderungsgeschwindigkeit (ΔI/Δt) der Stromstärke. Dann gilt also auch
| Uind = - L · ΔI/Δt (*) |
Je größer die Induktivität L, desto größer ist der Betrag der Selbstinduktionsspannung /Uind/ bei einer bestimmten Änderungsgeschwindigkeit der Stromstärke ΔI/Δt. (Auf das Vorzeichen kommt es hier nicht an.)
Die Induktivität L hat die Einheit [L] = 1 V·s/A = 1 H
("Henry"). {Vgl. mit der Einheit der Kapazität: [C] = 1
A·s/V = 1 F ("Farad")}.
Im Allgemeinen muss die Steigung des
t-I-Graphen durch die Ableitung der Stromstärke I nach der Zeit, also
dI/dt oder I· (gelesen I
punkt), ersetzt werden. So gilt allgemein:
| Die Selbstinduktionsspannung Uind ist proportional zur Zeitableitung der Stromstärke dI/dt = I·. |
(Wenn Widerstände im Stromkreis in Reihe mit der Spule liegen, treten Spannungsabfälle auf. Die Zusammenhänge zwischen Stromstärke und Spannungen sind dann weitaus komplizierter. Die Gesetzmäßigkeit (*) für die Selbstinduktionsspannung bleibt aber bestehen.)
Die Induktivität spielt bei der Selbstinduktion eine große Rolle.
Für eine lange Spule mit der Querschnittsfläche A, der Länge ℓ, der Windungszahl N kann man L berechnen:
| L = µ0·µr·A·N2/ ℓ |
wenn B = µ0·µr · I· n/ℓ . µ0 ist dabei die magnetische Feldkonstante, µr die relative Permeabilität.
**) Mit einer so
genannten Strompumpe
und einer geeigneten Spule (z.B. der Schülerversuchsspule
von 2 x 0,1 H mit je 1,5 Ω) ist das möglich.
.
( Mai 2014 )
Auch
das Video von einem